(Corrigé en-dessous de l'énoncé)
3éme
- CONTRÔLE DE CHIMIE - 1h00
Calculatrices autorisées |
24 septembre 2001
Ne recopiez pas les questions, mais
rappelez le numéro de la question.
Les exercices étant indépendants, vous pouvez les traiter dans l'ordre que vous voulez.
Exercice
1 :
Rappelez la
définition d’un atome. Quelle est
la taille moyenne d’un atome ?
Soit
l’atome de magnésium (Mg ; Z=12). Que représente Z ?
Quels sont
les constituants de l’atome de magnésium; quelles sont leurs charges électriques ?
Dessinez le
modèle de l’atome de magnésium (Mg ; Z=12).
Quels autres
modèles de représentation de l’atome connaissez-vous ?
Exercice
2 :
Quelle est la longueur correspondant à un
million d'atomes de cuivre de diamètre 0,26 nm, placés côte à côte ?
Exercice 3 :
Combien d’atomes de diamètre 10-10 m peut on mettre
côte à côte dans un fil de 1 mm ?
Chaque atome pouvant être considéré comme une petite sphère, quelle
distance, exprimée en km, représenteraient ces atomes si leur taille était non pas de
10-10 m mais de 1 cm ?
Exercice 4 :
Une feuille d’aluminium a 0,015 mm d’épaisseur. Chaque atome
est représenté par une sphère de 0,3 nm de diamètre.
Combien y a-t-il d'atomes d'aluminium dans cette épaisseur en
supposant qu'ils soient disposés les uns sur les autres ?
Exercice 5 :
Un atome de cuivre a une masse de 1,05 x 10-25 kg.
Combien y a-t-il d'atomes dans un kilogramme de cuivre? un gramme de
cuivre ?
Exercice 6 :
Les masses des atomes d’aluminium, de cuivre et d'étain valent
respectivement 4,48 x 10-26 kg, 1,05 x 10-22 g et 19,71 x 10-20
mg.
Exprimez ces masses atomiques avec la même unité de masse.
Classez ces masses par ordre croissant.
CORRECTION
Barème |
1 |
Exercice 1 :
Toute la matière, solide, liquide, gazeuse, est constituée d'atomes
; l'atome est la plus petite fraction de la matière..
|
| 1 |
- La taille moyenne d’un atome est de 10-10 m.
|
| 1 |
- Soit l’atome de magnésium (Mg ; Z=12). Z représente
le numéro atomique de cet atome, c'est à dire son nombre de protons (ou d'électrons).
|
| 1 |
- L’atome de magnésium est constitué d'un noyau entouré d'un
nuage de 12 électrons négatifs. Le noyau est lui-même constitué de 12 protons
(positifs) séparés par des neutrons(neutres).
|
| 1 |
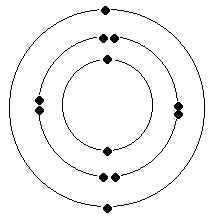
|
| 2 |
| 1803 |
John Dalton |
1er modèle |
petites sphères rigides |
1902 |
Thomson |
modèle fourré aux électrons |
l'atome est constitué d’une substance positive dans laquelle
baignent des électrons négatifs. |
| 1911 |
Rutherford |
modèle planétaire |
les électrons négatifs tournent autour d’un noyau positif comme les
planètes autour du soleil. |
| 1913 |
Bohr |
modèle quantique |
les électrons sont répartis en couches. |
| 1924 |
De Broglie et Born |
modèle probabiliste |
la densité des points signale la probabilité de trouver un électron
dans l'espace. |
|
| 2 |
Exercice 2 :
L’atome de cuivre a un diamètre de 0,26 nm soit 0,26 x 10-9
m.
Un million d’atomes = 106
atomes.
La longueur correspondante à 1 million d’atomes est :
l = nombre d’atomes x diamètre
d’1 atome
l = 106 x 0,26 x 10-9 = 0,26 x 10-3 m (= 2,6 x 10-4
m) = 0,26 mm
|
| 4 |
Exercice 3 :
Le nombre d’atomes est :
n = longueur du fil / diamètre d’1
atome = 10-3 / 10-10 =
10-3 x 1010 = 107 = 10 000 000 atomes.
Si la taille de ces atomes était de 1 cm, ces dix millions
d’atomes représenteraient une longueur de :
l = 107 x 1 =
107 cm = 107 x 10-2 m = 105 m = 105 x 10-3
m = 102 km = 100 km
|
| 2 |
Exercice 4
Épaisseur de la feuille = 0,015 mm = 0,015 x 10-3 m = 15 x 10-6
m
diamètre de l’atome = 0,3 nm = 0,3 x 10-9 m = 3 x 10-10
m
Le nombre d’atomes dans l’épaisseur est :
n = épaisseur de la feuille / diamètre
d’1 atome
n = 15 x 10-6 / 3 x 10-10
= 5 x 10-6 x 1010 =
5 x 104 = 50 000 atomes.
|
| 3 |
Exercice 5
Le nombre d’atomes est :
n = masse totale / masse d’un atome
n = 1 / 1,05 x 10-25 = 0,952 x 1025 = 9,52 x 1024
atomes
Dans 1 gramme, il y en aura 1000 fois moins : 9,52 x 1021
atomes
|
| 2 |
Exercice 6
Exprimons tout en kg :
masse de l’aluminium : 4,48 x 10-26 kg
masse du cuivre : 1,105 x 10-22 g =
1,105 x 10-22 x 10-3 kg = 1,105 x 10-25
kg
masse de l’étain : 19,71 x 10-20 mg = 1,971 x 10-19 mg = 1,971 x 10-19
x 10-6 kg = 1,971 x 10-25 kg
En classant ces masses par ordre croissant (du plus petit au plus
grand), on a :
4,48 x 10-26 kg < 1,971 x 10-25 kg< 1,105 x
10-25 kg
aluminium < cuivre < étain
|
|